Helpful Junit methods

Figure 369. Available comparison methods

Figure 370. Caution comparing float / double !!

Figure 371. Weird arithmetics?

org.opentest4j.AssertionFailedError: expected: <3.6> but was: <3.5999999999999996>
            ...
        at de.hdm_stuttgart.AppTest.test1_3(AppTest.java:35)

Figure 372. Limited representation precision

IO.println("3.6 - 3 * 1.2 == " + (3.6 - 3 * 1.2));

Result:

3.6 - 3 * 1.2 == 4.440892098500626E-16

Figure 373. Solving the issue

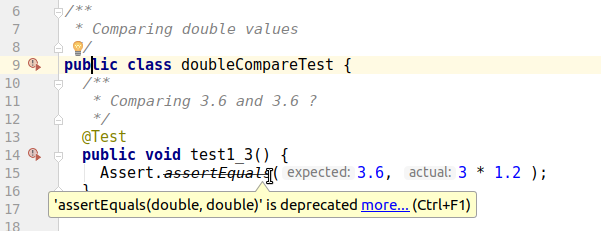
public class doubleCompareTest {
  static final double delta = 1E-15;
  /**
   * Comparing 3.6 and 3 * 1.2 within delta's limit
   */
  @Test
  public void test1_3() {
    Assertions.assertEquals(3.6, 3 * 1.2 , delta);
  }
}

exercise No. 138

Summing up integers to a given limit

Suppose an arbitrary number n is given e.g n=5. We want to compute the sum of all integers ranging from 1 to 5:

1 + 2 + 3 + 4 + 5 = 15

Unzip task.zip and import the resulting Maven project into your IDE. Then implement getSum (int limit) in class Summing.

Generate the Javadoc and read the description of getSum (int limit).
Implement the method
Test your implementation by executing SummingTest.

solution.zip

exercise No. 139

Summing up, the better way

The previous solution of Summing up integers to a given limit suffers from a performance issue. When dealing with large values like 65535 looping will take some time:

long start = System.nanoTime();
IO.println("1 + 2 + ... + 65535" + "=" + getSum(65535));
long end = System.nanoTime();
IO.println("Elapsed time: " + (end - start) + " nanoseconds");

1 + 2 + ... + 65535=2147450880
Elapsed time: 1169805 nanoseconds

Barely more than one millisecond seems to be acceptable. But using the method for calculations inside some tight loop being executed millions of times might have a serious performance impact.

Thus improve your previous solution avoiding the loop by using the explicit form. When you are finished re-estimate execution time and compare the results.

Tip

Read “Techniques for adding the numbers 1 to 100”.

solution.zip

Prev	Up	Next
Parameterized testing	Home	Technical details

Unit testing